The previous section summarized the 10 steps for developing and implementing an on-farm research project. In steps 1 through 3, you wrote out your research question and objective, developed a hypothesis, and figured out what you will observe and measure in the field. Now you are ready to actually design the experiment. This section provides more detail on step 4 in the process.
Recall from the introduction that on-farm research provides a way of dealing with the problem of field and environmental variability. In comparing the effects of different practices (treatments), you need to know if the effects that you observe in the crop or in the field are simply a product of the natural variation that occurs in every ecological system, or whether those changes are truly a result of the new practices that you have implemented.
Take the simple example of comparing two varieties of tomatoes: a standard variety and a new one that you have just heard about. You could plant half of a field in the standard variety and the other half of the field in the new variety. You plant the tomatoes on exactly the same day, and you manage both halves of the field exactly the same throughout the growing season. Throughout the harvest period, you keep separate records of the yield from each half of the field so that at the end of the season you have the total yield for each variety. Suppose that under this scenario, the new variety had a 15 percent higher yield than your standard variety. Can you say for sure that the new variety outperforms your standard variety? The answer is no, because there may be other factors that led to the difference in yield, including:
- The new variety was planted in a part of the field that had better soil.
- One end of the field was wetter than the other and some of the tomatoes were infected with powdery mildew.
- Soil texture differences resulted in increased soil moisture from one end of the field to the other.
- Part of the field with the standard variety receives afternoon shade from an adjacent line of trees.
- Weed pressure is greater in one part of the field with the standard variety.
- Adjacent forest or wildlands are a source of pests that affect one end of the field more than the other.
With the right experimental design and statistical analysis, you can identify and isolate the effects of natural variation and determine whether the differences between treatments are “real,” within certain levels of probability. This section looks at three basic experimental design methods: the paired comparison, the randomized complete block and the split-plot design. Which one you choose depends largely on the research question that you are asking and the number of treatments in your experiment (Table 2).
The number of treatments in your experiment should be apparent from your research question and hypothesis. If that is not the case, then you will need to go back and refine your research question so that you have more clarity as to what you are testing. As previously noted, when identifying your research question (step 1), remember to keep things simple. Avoid over-complicating your experiment by trying to do too much at once. And, keep in mind that although the randomized complete block and split-plot designs provide more information than the paired comparison, they also require a larger field area, more management and more sophisticated statistics to analyze the data. Table 2 also lists the type of statistical analysis associated with each experimental design method. These statistical techniques are covered in the next section, Basic Statistical Analysis for On-Farm Research. First is a review of some basic experimental design terminology.
TABLE 2: Three Experimental Design Methods
| DESIGN METHOD | WHEN TO USE | STATISTICAL ANALYSIS |
| Paired comparison | To compare two treatments | t-test |
| Randomized complete block | To compare three or more treatments | Analysis of variance (ANOVA) |
| Split-plot | To see how different treatments interact | Analysis of variance (ANOVA) |
Treatments: A treatment is the production practice that you are evaluating. Examples of treatments include choice of variety, different fertilizer rates, different fertilizer timing, choice of cover crops, different cover crop management strategies, timing of planting, type of tillage, different pest control methods or different irrigation strategies. For animal operations, treatments might be different feed rations, type of bedding, pasture versus confinement, grazing period, nutritional supplements, or disease/parasite controls. The choices are limitless given the complexity of farming. On-farm research usually compares just two or three practices. In most cases, one of the treatments is the standard practice, or what you usually do, and is known as the “control.”
Small-scale intensive onion production on plastic in Interlaken, NY. Cornell extension vegetable specialist Christine Hoepting found growers could improve yields and reduce bacteria incidence by using alternatives to black plastic mulch, and by increasing planting density. Courtesy Cornell University Cooperative Extension
Variable: In statistics, a variable is any property or characteristic that can be manipulated, measured or counted. In on-farm research, the independent variable is the different treatments (practices) you are applying, and the dependent variable is the effect or outcome you are measuring. What you measure in your particular experiment depends on what treatments you apply. Examples include crop yield, weed density, milk production or animal weight gain.
Plot: Plots are the basic units of a field research project—the specific-sized areas in which each treatment is applied. Replication: Replication means repeating individual treatment plots within the field research area. If you set up an experiment comparing two treatments, instead of setting out just one plot of Treatment A and one plot of Treatment B, you repeat the plots within the field multiple times. Replications reduce experimental error and increase the power of the statistics used to analyze data.
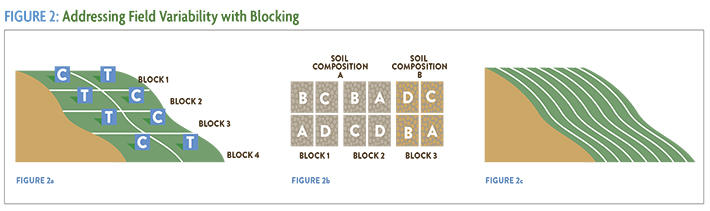
Block: It is usually not possible to find a perfectly uniform field in which to conduct the experiment, and some sources of variation simply cannot be controlled (e.g., slope or soil texture gradients). In order to address the problem of field variability, divide your field of interest into sections that have common slope and soil characteristics. Within each section—typically known as blocks—field conditions should be as uniform as possible. Taken together, however, all of your blocks should encompass the variability that exists across the research area. After delineating the areas for your blocks, make sure you include each treatment inside each block; that way, your blocks can serve as replications. In most on-farm research studies, four to six blocks are sufficient to provide a good level of confidence in the results. Figure 2 provides examples of how to use blocking to address field variability due to slope or soil type.
Agricultural research should usually be blocked because of field variability. If your field has a known gradient, such as a fertility or moisture gradient, it is best to place blocks to that conditions are as uniform as possible within each block. Figure 2a: On a slope, for example, each whole block should occupy about the same elevation. Treatments are randomized and run across the slope within each block. Figure 2b: Place whole blocks within different soil types. Figure 2c: If blocks cannot be used to account for variability, then each treatment should run across the whole gradient, as in all the way down the slope or all the way across the field. This arrangement can also be used for a completely randomized design (see Figure 3).
Randomization: In addition to replication, randomization is also important for addressing the problem of field variability, reducing experimental error and determining the true effect of the treatments you are comparing. Replications should be arranged randomly within the field. Or in the case of a blocked experimental design, treatment plots must be arranged randomly within each block. If you have three treatments, for example, you cannot place those treatments in the same left-to right sequence within each block. They must be arranged in a random order. This can be done using the flip of a coin, drawing numbers from a hat or using a random number generator for each block.